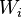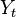[출처: 나, 블로그 연구, 그 첫번째 이야기 #2]
우리는 흔히 무언가를 말하거나 자신의 주장을 펼치때 손쉽게 사용하는 방법으로 "비교법"을 사용한다.
비교라는 것은 비교대상의 특정 부분을 원대상과 견주어 놓고서 비교하는것며, 비교를 통해서 우리가 이전에는 잘 인지 못하였던 부분이나 어떠한 경향을 쉽게 도출해낼수가 있다.
그래서 생각해보았다.
(먼저, 생각이라는 것은 연구를 하기 위한 가장 기본적인 도구이다. "어떻게 생각하는가?" 가 해당 테스크의 퍼포먼스를 결정하고, 그 일을 앞으로 올바른 방향성으로 이끌어 가기도 한다. 따라서 이제부터, 말하는 생각이라는 단어는 단순히 생각이 아니라 수 많은 고민과 다양한 직관력을 가지고서 대상을 분석하고 연구를 하는것이라고 전제하겠다)
나는 주로 마인드맵식 나열법이라고 생각의 덩어리들을 자유롭게 풀어놓는 방법을 사용한다.
그리고 이들간의 연관성을 찾아서 서로 연결하고 분류하여 새로운 그들만의 그룹을 만드는 작업을 하고 이들 그룹에는 대표성을 지는 이름을 붙인다. 이 이름이라는것은 아직 정형화되지 않는 나의 생각을 하나의 개념으로 한정짓는 작업이기에 자칫하면 생각의 방향성을 고정시킬수가 있다. 따라서 신중을 기해서 태깅을 해야한다. 다시 본론으로 돌아가서, 나는 아래와 같은 절차를 거쳐서 생각해보았다. 그리고 답을 달수있는 부분에서 "->" 를 넣어서 나 스스로 답을 달아 보았다.
*앞으로 계속해서 답을 채워나갈 예정이다*
1) 어떻게 하면 기존 블로그들의 특징을 잘 분류할수있을까?..
2) 주제를 한정시켜서 쉬운 분류작업부터 시도해볼까?
3) 혹시 나와같은 생각을 가진 기존 사례는 없었는가? 여기에 해답이 없겠는가?
-> 만약있다면..그리고 아주 뛰어난 분석과 결론이 도출되었다면, 본 연구는 접어야 한다..ㅠㅠ 이는 선행조사라고 할수 있으며 무언가를 연구를 하는 동시에 내가 목표로하는 것과 동일의 주제가 존재하는지 혹은 경쟁적인 연구사례가 존재하는지 찾아보는 것으로 연구를 위해서 매우 중요하다. 하지만 본 "블로그 탐구"에서는 그저 탐구만을 하기로 했기에 기존 사례가 존재하더라도 무시하고 오히려 참고하여 [날마다 연구]를 끝까지 해보도록 하겠다.
4) 블로그의 게시글들의 공통점은 무엇인가?
5) 효과적인 블로그 글들의 검색방법은 무엇일까?
6) 상위 검색 글들은 어떤 비밀이 숨겨져 있는가? (글의 패턴, 글자수, 그림의 수, 공백의 크기 등등)
7) 네이버에서의 상위글들과 다음에서의 상위글들은 어떻게 다른가? 그렇다면 구글은?
8) 블로그의 랭킹은 어떻게 달라지는가?
9) 블로그 유입자를 늘리기 위해선 무엇이 필요한가?
10) 블로그의 정의란 무엇일까?... 블로그를 하는 사람의 마인드는? 목적은?...블로그를 찾는 사람의 마음은?
11) 우리는 주로 언제 블로그를 찾거나 블로그를 하는가?
12) 블로거 (블로그를 유지 보수 하는 온라인사용자) 들의 유형은? 타입은?
13) 그들은 주로 언제 글을 쓰는가?
14) 글의 주제에 따른 태그는 무엇을 다는가?
15) 파워블로거들의 분포는? 네이버, 다음, 티스토리 등등..
16) 검색엔진들이 친철하게 대해주는 유입자들은? 블로거들은?
17) 검색엔진들 (네이버, 다음, 구글 등등) 의 관점에서 바라본 블로그의 글들은 무엇일까?
18) 그날의 인기글이 되는 비법은? 상위 노출의 비밀! 또한 왜 쓸데없는 정보를 가진 글들이 상위에 노출되는가? (낚시글)
19) 방문자들의 관점에서 바라본 블로그
20) 상업성 블로그와 취미 블로그의 구별법?
최대한의 연상 생각법(하나의 생각들이 꼬리를 물고 늘어지면서 확장되고 다양한 아이디어를 창출할수 있는 방법. 기존의 연상기억법에 착안) 을 통하여 위와 같은 질문들을 짧은시간 약 10분만에 도출해냈다. 이제 이 간단한 몇가지들의 질문들을 다시 재분류하고 쓸만한 정보와 앞으로의 방향성들을 찾아보면 아래와 같다.
그룹화 -> 간결화 - > 주제 도출 -> 앞으로의 방향성 도출
[Group1: 인과 관계에 따른 분석이 필요함]
5), 8), 11)
[Group2: 특이성을 도출해야함]
6), 7), 9), 16), 18)
[Group3: 나름의 정의를 내려야 함]
1), 2), 12), 17), 19)
[Group4: 유사사례 검색법]
3), 4), 10), 13), 14), 15), 20)
위의 4가지 그룹화가 가능했으며, 이들에 대한 블로그 분석에 대한 아이디어들은 아래와 같은 순서로 진행될때 가장 좋은 효과를 보일것 같다.
G3 - G4 - G1 - G2
그리고 결론적으로 이들 블로그의 분석을 통하여 지향하는 것은 단순히 "파워 블로그가 되는법"을 찾는것이 아니라 "파워 블로그처럼 유익한 글들을 포스팅하는 법"이 될것이다. 따라서 이제부터 위의 질문들에 대한 답들을 찾아볼 것이다.
'Any Notion > Routine laboratory ' 카테고리의 다른 글
| [날마다 연구] #1 블로그로의 분석적 접근 (0) | 2014.12.03 |
|---|




![0 < \mathbb{E}[S_i] < \infty.](http://upload.wikimedia.org/math/6/4/2/642646acd87e01cd6befabcb8ba03731.png)
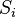

![\mathbb{E}[S_i]](http://upload.wikimedia.org/math/9/2/e/92e2d7bbd26c3eb3dfb9666dad1b61a3.png)
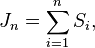


![[J_n,J_{n+1}]](http://upload.wikimedia.org/math/6/b/e/6bec9ae0b54f0d735f3511a0aa7f0507.png)