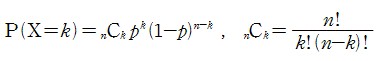[independent identically distribution] 독립 동일 분포

In probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed (i.i.d.) if each random variable has the same probability distribution as the others and all are mutually independent.[1]

The abbreviation i.i.d. is particularly common in statistics (often as iid, sometimes written IID), where observations in a sample are often assumed to be effectively i.i.d. for the purposes of statistical inference. The assumption (or requirement) that observations be i.i.d. tends to simplify the underlying mathematics of many statistical methods (see mathematical statistics and statistical theory). However, in practical applications of statistical modeling the assumption may or may not be realistic. To test how realistic the assumption is on a given data set, the autocorrelation can be computed, lag plots drawn or turning point test performed.[2] The generalization of exchangeable random variables is often sufficient and more easily met.

The assumption is important in the classical form of the central limit theorem, which states that the probability distribution of the sum (or average) of i.i.d. variables with finite variance approaches a normal distribution.

Note that IID refers to sequences of random variables. "Independent and identically distributed" implies an element in the sequence is independent of the random variables that came before it. In this way, an IID sequence is different from a Markov sequence, where the probability distribution for the nth random variable is a function of the previous random variable in the sequence (for a first order Markov sequence). An IID sequence does not imply the probabilities for all elements of the sample space or event space must be the same.[3] For example, repeated throws of loaded dice will produce a sequence that is IID, despite the outcomes being biased.

줄여서 i.i.d.는 어떠한 랜덤 확률변수의 집합이 있을때 각각의 랜덤 확률변수들은 독립적이면서 (자기 사건의 발생의 영향이 다른 랜덤 확률변수에게 미치지 않을 때) 동일한 분포를 가질때를 의미한다.

예를들어서, 이항확률 분포 (성공 or 실패)를 가지는 동전던지기를 3회 실시한다고 가정하자.

각각의 시행은 이전이나 이후의 시행에 영향을 주지않는 독립시행이며 각각의 시행에서 나오는 동전의 앞,뒤에 대한 결과값의 분포는 동일한 이항확률 분포를 따르기 때문에 이는 i.i.d.라고 할수 있다.

정규분포가 연속변량인 데 대하여 이항분포는 이산(離散)변량이다. 어떤 시행에서 사건 A가 일어날 확률을 p, 사건 A가 일어나지 않을 확률을 q(=1-p)라 한다. 이 시행을 독립적으로 n회 되풀이할 때, 그 중에서 k회만 A가 일어날 확률은 n!/(k!(n-k)!)·p^kq^n-k (k=0,1,…,n)이다. 예를 들어 주사위를 한 번 던져서 1의 눈이 나올 확률을 1/6이라 하면, 5회 되풀이하여 던졌을 때 1의 눈이 2회만 나올 확률은 5!/(2!3!)·(1/6)²·(5/6)^5-2≈0.16이다.

이와 같이 X가 0에서 n까지의 값을 취하는 확률변수라 할 때, X가 k일 확률 P(X=k)가

평균값 m은 m=np, 분산 σ²은 σ²=npq(q=1-p)이다. 그리고 p가 0이나 1에 가깝지 않고 n이 충분히 크면 이항분포는 정규분포(가우스분포)에 가까워지며, p가 1/2에 가까워짐에 따라 그래프는 좌우대칭인 산 모양 곡선이 된다.

한편, 이항정리에 따라 (p＋q)ⁿ을 전개하면 다음과 같다.

[네이버 지식백과] 이항분포 [binomial distribution, 二項分布] (두산백과)

이항분포 참조 : http://terms.naver.com/entry.nhn?docId=1135793&cid=40942&categoryId=32215

만약 이를 코드화나 모델링화 시킨다면, 변수의 값을 선택할 때 정의된 동일한 확률분포에서 표본을 선택한다면 이를 i.i.d.한 확률 표본이 된다고 할수가 있다.

[출처] 확률변수의 결합 - 확률표본|작성자 isabella