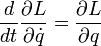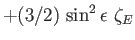N.&C./Optimization

A Tutorial on Cross-Layer Optimization in Wireless Networks 2013.07.23
[Lagrangian] 라그랑지언 2013.07.09
LMS 알고리즘 2013.06.10 1

A Tutorial on Cross-Layer Optimization in Wireless Networks

2013. 7. 23. 10:00

**본 논문은 제가 따로 요약 하였기에 저작권법에 접촉되지 않습니다.

(IEEE JOURNAL ON SELECTED AREAS IN COMMUNICATIONS, VOL. 24, NO. 8, AUGUST 2006)

A Tutorial on Cross-Layer Optimization in Wireless Networks

Xiaojun Lin, Member, IEEE, Ness B. Shroff, Senior Member, IEEE, and R. Srikant, Fellow, IEEE

-Tutorial Paper-

Abstract-

이 Tutorial paper는 최근의 무선시스템에서의 자원배분 문제 최적화 기법에 대한 발전에 대해서 보여준다.

1)우리는 Cellular networks(single hop) 를 위한 ‘opportunistic (channel-aware) scheduling’ 영역의 중요한 결과들을 살펴봄으로써 시작했다. 왜냐하면, Cellular networks은 성능 최적화가 많이 필요한 영역이기 때문이다.

우리는 배웠던 중요한 교훈들을 설명하고 2)multi-hop wireless networks에서의 일반적인 자원배분 문제들에 대한 주요한 문제점들에 대해서 이야기 할 것이다.

그리고 Tutorial이 뒷부분에서는 3) loosely coupled” cross-layer solution 안에서의 깔끔하게 최적화문제로 풀어낸

Multi-hop resource allocation problem naturally results를 보여 줄 것이다.

이 말의 의미는, 하나의 알고리즘으로써 서로 다른 Protocol stack의 Layer층 (예를 들면, MAC/ PHY)에 대한 map을 얻는 것이기도 하며, 송수신되는 정보 (왔다갔다하는)를 통해서 결합되는 알고리즘을 의미한다.

이 알고리즘은 바로, 매우 복잡한 MAC층에서의 최적화된 스케줄링 구성요소로 취급될 것이고, 분산되는 간단한

솔루션들이 필요하다. 그리고 우리는 어떻게 Cross Layer framework에서 불완전한 스케줄링을 사용할 것인지를 시연하고, 최근에 개발된 분산 알고리즘에 대해서도 알아 볼 것이다. 그리고 마지막으로 우리는 a set of open research problems을 토의함으로써 마칠 것이다.

즉, 다시 말해서 위 논문은 아래의 5가지 단계를 따른다.

1) 기회주의적 스케줄링을 살펴봄

2) 멀티 홉 무선네트워크에서의 자원배분 문제를 알아봄

3) 위의 자원배분 문제를 Loosely-coupled 된 Cross Layer에서 다시 자원배분 문제를 접근함

4) 그리고 어떻게 불완전한 스케줄링 알고리즘을 사용했는지, 분산 알고리즘은 무엇인지 설명 할 것이다.

5) 마지막으로 이와 함께 고민할 수 있는 Open Problems을 다룸으로 마친다.

1. 기회주의적 스케줄링 ‘Opportunistic scheduling’ 의 의미는?

무선시스템은 무선채널의 시변특성, 한정된 자원의 공유, 페이딩 등의 특성으로 인해 유선시스템과 비교할 때 높은 대역폭을 사용자들에게 제공하기에 어려운 문제점들을 안고 있다. 이러한 문제점을 해결하기 위해 제시된 무선채널에서의 스케줄링 방법이 Opportunistic Scheduling (기회주의적 스케줄링) 또는 Channel-Aware Scheduling 방식이다

기회주의적 스케줄링이란 하나의 엑세스 포인트가 여러 사용자를 TDMA 방식을 통해 동시에 수용할 경우, 매 타임슬롯마다 가장 채널 상태가 좋은 사용자들을 “기회주의”적으로 선택하여 서비스를 제공하는 방식을 말한다. 기존의 방식에서는 사용자들의 채널정보를 알지 못하기 때문에 정적인 시분할 방식을 사용하였다. 그에 따라 채널속도가 빠르지 않은 사용자가 채널을 점유할 경우, 그 효율이 떨어지는 단점이 있었다. 이를 극복하기 위해서 매 타임슬롯마다 사용자들이 자신의 채널정보를 엑세스 포인트로 피드백하고, 엑세스 포인트는 각 사용자들로부터 받은 정보를 토대로 가장 좋은 채널상태를 갖는 사용자를 골라서 서비스를 하게 된다.

기회주의적 스케줄링을 구현하는 방법에 있어서 시스템의 처리량을 최대화하는 방식과 사용자간의 공평성을 맞추는 방식 사이의 적절한 조화를 위한 노력이 있어왔으며 또한 QoS와 best effort 트래픽을 동시에 지원하기 위한 노력이 있어왔다. 반면, 현재까지 개발된 많은 알고리즘들은 사용자수가 변하지 않고 각 사용자들의 큐가 다 비워지지 않는다고 가정하는 패킷레벨에서의 방식들이었다. 반면, 실제 시스템에서는 각 사용자들의 트래픽이 유한한 서비스 시간 또는 파일사이즈를 갖고 큐에 랜덤하게 도착하고 서비스를 다 받으면 큐를 떠나게 된다. 이를 효과적으로 분석하기 위해서는 패킷레벨에서의 분석 대신 플로우 레벨에서의 분석이 필요하다. 그에 따라, 본 논문에서 다루는 것이 기회주의적 무선시스템에서의 QoS와 best effort 트래픽의 통합과 그에 따른 문제점의 플로우레벨에서의 분석이다.

Q. 논문의 이해를 위해서 고민해봐야 하는 내용들

-Cross-Layer의 의미는?

OSI7과 같은 Independent layers의 독립적인 rule을 break 하는 것이다. 왜냐하면, 이를 통하여 비약적인 성능의 향상의 결과가 있기 때문이다. 방법론적으로, 다른 layers 간의 변수공유와 같은 방법이 존재한다. 디자인 형태는 6가지가 존재하며, 내부적인 feedback 과 상호작용은 3가지 형태로 요약이 가능하다.

- 분산 알고리즘이란? ‘Distributed Algorithm’

A distributed algorithm is an algorithm designed to run on computer hardware constructed from interconnected processors. Distributed algorithms are used in many varied application areas of distributed computing, such as telecommunications, scientific computing, distributed information processing, and real-time process control. Standard problems solved by distributed algorithms include leader election, consensus, distributed search, spanning tree generation, mutual exclusion, and resource allocation.[1]

I. INTRODUCTION

Optimization-based 의 접근법은 지금까지 통신 네트워크 영역에서 “Resource allocation problem” 해결을 위해서 광범위하게 연구 되어왔다. 예를 들면, Internet congestion control은 시스템의 성능을 최대한으로 끌어내는 convex optimization problem 으로 distributed primal or dual solutions 자원배분문제를 어떻게 해결하는가 에 대한 모범적인 예로써 생각할 수가 있다. 이런 류의 접근법(실험법) 은 TCP(transmission control protocol)에 대한 깊은 이해와 향상된 혼잡제어(congestion control) 라는 솔루션을 보여준다.[1-6]

어쨌든 질문의 핵심은 앞서 말한 접근법이 통합된 multi-hop wireless networks에서 *a clean-slate design of the protocol stack으로 적용 될 수 있다는 점이다. 사실, Internet setting 에서의 그러한 기술의 직접적인 어플리케이션을 허용하지 않는 무선통신의 맥락에서 있어서 꽤 특별한 도전들이 있다. 특히, 무선매체는 본질적으로 유저들의 데이터송신에 의한 간섭이 많이 일어나는 다중접속매체로써, 채널의 capacity가 time-varying 의 성격을 보인다. 이러한 이유로, 무선매체는 사용자와 네트워크 Layer간의 상호의존성을 띄기 때문에 기존의 유선과는 반대의 성격을 가진다. 하지만, 이런 어려움에도 불구하고, 최근에 통합 및 최적화된 형태로써의 Multiple layer들의 무선자원을 자유로이 공유하거나 넘나드는(Cross Layer개념) 진보된 결과들을 보여준다. 이와 관련된 흥미로운 내용은 섹션3에서 설명한다.

(The solution of such an optimization framework will itself exhibit a layered structure with only a limited degree of cross-layer coupling.)

*The notion of a clean-slate design becomes especially attractive for multi-hop wireless networks, where the burdens of legacy systems are far less than for the Internet.

*Protocol Stack : 서로 다른 기기들이 데이터 통신을 하는 데 필요한 통신 규약을 구현해 주는 소프트웨어 모듈들의 모임. 즉, 각 기기 간에 통신을 할 때 해당 통신 규약을 구현해 주는 핵심 소프트웨어이며, 프로파일은 상호 접속성을 확보하기 위해 애플리케이션에서 사용해야 할 통신 규약을 규정한 것이다. 예를 들어, 노트북 컴퓨터와 휴대 전화가 통신하기 위해서는 통신 규약이 서로 맞아야 데이터를 교환할 수 있다. 통신 규약 스택은 각각의 하드웨어에 탑재되어 통신 규약을 맞추어 구현해 주는 역할을 담당한다. 대표적인 것으로 TCP/IP 스택이 있으며, 이는 윈도즈 운영 체계에 포함되어 있다.

우리는 use of such an optimization approach for two classes of cross-layer problem을 분명히 보여 줄 것이다. 즉 다시 말해서,

Cellular 망(or access-point-based single-hop networks)에서 기회주의적 스케줄링 문제점을 보고 시나리오를 발전시켜서 multi-hop wireless networks에서의 혼잡제어와 스케줄링 문제를 살펴볼 것이다.

그리고 optimization approach를 해결하기 위한 중요한 도구로 사용되는 convex programming 에 대해서 알아볼 것이다.

; 특히, convex programming에서 Lagrange duality은 복잡한 최적화 문제를 간단한 여러 가지 문제로써 분해하는 중요한 핵심 도구이다. 하지만, 우리는 종종 우리는 이것만으로 문제를 100% 해결하는 것에는 부족하단 것을 안다. 왜냐하면, 유선 네트워크와는 반대로, 많은 무선 네트워크에서의 Cross-layer control problems 은 not convex (볼록) 않기 때문이다.

예를 든다면, 무선 네트워크에서의 간섭문제들로 인하여, 각각의 시간에 대해서 활성화 되어야 하는 링크들의 부분집합들에 대한 선택에 있어서 정확히 선택해야 하는 정교한 스케줄링 mechanisms을 요구하는 것 같은 것이다. 무선 네트워크에서, 각 링크들의 capacity는 신호와 간섭레벨에 의존적이고, 그러한 것들은 파워와 링크의 전송 스케줄에 의존적이다. 그래서 link capacity, power assignment, and the transmission schedule 에서의 관계들은 전형적으로 non-convex 하다.

그러므로, 스케줄링 요소는 어려운 non-convex problem을 풀기 위해 필요하고, 이는 보통 전체 솔루션에서 병목현상을 뛴다.

무선 네트워크에서 이러한 문제들을 내재하는 non-convex 문제들을 해결하기 위해선, convex-programming 적인 진보된 테크닉의 사용이 요구된다.

이 tutorial paper에선, 아래의 6가지 예시들을 집중적으로 살펴 볼 것이다.

1) Tools from convex programming,

2) Combinatorial optimization

3) Stochastic stability

4) Graph theory

5) Large deviations

6) Heavy-traffic limits are used to obtain realistic and efficient solutions to the cross-layer control problem.

cross-layer optimization 는 최근 사이에 꽤 큰 이슈로 발전 되었고, 이를 위한 포괄적인 조사는 공간적인 (space constraints) 제한을 가진다. 따라서, 이 paper에선 모두를 다 조사하진 못했다. 오히려, 포커스는 주요한 이슈와 도전들, 그리고 테크닉과 open problem들에 대해서 독자들에게 알려주는 정보전달에 대해서 맞춰져 있다. [7]을 참조하길 바란다.

본 논문의 구성은 아래와 같다.

Section II: cellular networks에서 scheduling 문제점에 대한 설명을 하면서, 스케줄링 선택에 있어서 물리계층 채널 정보를 결합시키는 점에 대해서 강조한다.

Section III: we investigate the joint congestion-control and scheduling problem in multi-hop wireless networks.

섹션3의 내용은 주로 the cross-layer problem 를 a congestion control component and a scheduling component 2가지로 깔끔하게 분해하며 접근한다. 하지만, non-convexity성격 때문에 실제 네트워크에서 스케줄링은 매우 어렵지만 cross-layer solution으로 심플하지만 불완전한 해결법으로 어느 정도 접근해본다.

Section IV: 당연히 이 부분은 앞으로 더 보완되고 다듬어져 가야 한다.

Section V: recent developments in obtaining imperfect distributed scheduling policies with provably achievable throughput bounds.

We then conclude with a set of open problems.

II. OPPORTUNISTIC SCHEDULING FOR CELLULAR WIRELESS NETWORKS

오랫동안 multiuser scheduling problem은 산업과 학교에서 많은 조명을 받아왔다. 그리고 multiuser scheduling problem은 무선 네트워크에서 독특한 특징으로써 많은 동기부여를 받아왔다. : 자원의 크기, mobile 유저의 간섭문제, 시변 채널의 조건들(이동성과 페이딩으로 인한)

좋은 스케줄링 방법이란, 높은 네트워크 성능을 만족시키는 채널 컨디션을 기회주의적 형태로 분석 활용하는 것을 의미한다.

예를 들면, N명이 이용자들과 베이스 컨디션으로 구성된 cellular networks를 고려하는 것이다.

게다가, 가정해보자. 유저들의 base station 으로부터의 타임슬롯시스템과 다운링크 통신에 대해서 가정해보자.

base station은 채널 조건을 기반으로 어느 유저가 전송이 가능한지 결정할 수가 있다. 이 아이디어는 SINR기반의 채널컨디션에 따라서 수신 단으로의 전송을 베이스 스테이션이 주어진 BER을 만족시키며 높은 속도로 전송을 허용하는 것을 의미한다. 이것은 Base Station 이 기회주의적 기법으로, 즉 높은 네트워크 성능유지를 위하여 채널의 조건을 이용한다는 의미이다.

이와는 달리 기존의 전통적인 방법에선, 채널의 가변성을 제거하는 것이 주된 관심사였다.

(예를 들면, spread spectrum, repetitive coding, and power averaging)

Opportunistic scheduling 에 대한 설명~ (앞장참고)

우리의 초점은 Downlink에서의 base station 전송 시나리오로 한정하며, 유/무한 backlogged cased을 위한 Opportunistic scheduling solutions을 볼 것이다.

A. Infinite-Backlog Case

Infinite-Backlog Case 종종 통신시스템 분야에서 프로토콜의 성능평가와 최대의 성능 량을 보기 위하여 사용된다.

이는 매우 심플하고 중요한 이해를 제공하는 다루기 쉬운 평가방법이다. 이 단락의 내용에서의 목적은 실행가능한 스케줄링 정책 Q를 찾는것이다. Q는 주어진 공정성과 QoS 요구조건을 만족하며, 전반적으로 시스템 성능이 최대화를 보여주는 스케줄링 정책을 의미한다.

: policy Q의 Vector.를 의미한다.

: The index of the user selected for transmission : 전송을 위한 선택되는 유저의 인덱스

: The data rate transmitted to user ; 사용자에게 전송되는 통신속도

Ui : the utility function of user , ; 유저의 이용률 함수

: measures the value or benefit to user i of the receiving data rate xi. ; i번째 유저의 수신속도 xi의 이익 또는 값의 측정값

(Note that xi is a function of the channel condition and the coding and modulation scheme used.)

There have been many scheduling schemes that address this problem [9]–[13].

그리고 흥미롭게도 이들의 심플하고 근시안적인 스케줄 정책들의 형태는 아래의 식으로 표현이 될 수가 있다.

and constants and can be viewed as Lagrange multipliers. For example, consider the following problem studied in [12], [13]:

*Lagrange Multipliers: 출력물 참조

: The set of all stationary scheduling policies,

: The minimum fraction of time-slots assigned to user (i.e., fairness in time)

명백하게 이것은 비선형 최적화 문제를 나타낸다. 하지만, 이것을 위의 Q*식에서 = 0과 의 적절한 값의 선택으로 최적화를 쉽게 보여준다.

Q*식의 최적화 법은 각각의 타임슬롯에서 실행되고, 는 확률적인 근사적 알고리즘을 통하여 얻을 수가 있다. [13]

유사하게도, temporal fairness 대신에 우리는 아래와 같은 QoS form을 고려할 수가 있다.

• Fairness in utility: Each user receives at least a fraction of the aggregate utility value [11], [13].

• Minimum data rate requirement: Each user receives a minimum data rate of bps [13].

• Proportional fairness: Here, the objective is to achieve a solution that is proportionally fair, i.e., increasing the mean throughput of one user from the optimal level by results in a cumulative percentage decrease by greater than of the mean throughput of other users [14]. It turns out that such a solution is achieved when the optimization problem is to maximize the sum of the logarithms of the expected rates (or the product of the expected rates), i.e.,

식을 통하여 도출되는 각각의 케이스는 Q*의 식과 상응하는 동일한 최적화 솔루션을 보여준다. (=0일 때)

그러므로, 이런 결과는 우리에게 무선네트워크상에서 시스템 성능의 기회적인 향상으로 이용될 수 있는 심플하면서 근시안적인 지표의 스케줄링 정책이라고 말해준다.

B. Stability of Opportunistic Scheduling Schemes

이전에 A에서는 Infinite-Backlog Case 의 시스템으로 가정하여서 QoS/fairness constraints 조건하에 시스템의 Utility를 평가하는 문제였다.

이제는, opportunistic scheduling을 좀더 발전시켜서, 시스템의 QoS 제한성과 안정성을 위배하지 않는 범위 내에서 다루는 문제를 볼 것이다.

먼저, 여기에 확률적인 안정성에서 유용성의 최대화로부터 이동한 문제가 있다. 이 문제는 throughput-optimal scheduling로 크게 관심 받아왔다. [15]

이 것은 최대화의 큐 가중치의 합의 비율이 바로, 최적의 처리량을 나타낸다는 스케줄링 법을 보여준다. 그리고 cellular networks에서, 이 스케줄링 법은 아래의 형식을 따른다.

: the queue length of user ,

xi : again the data rate transmitted to user

위의 스케줄링은 공정한 걸로 간주되며, 이것은 큐의 길이 정보가 최적화된 스케줄링 법에서 매우 중요한 것이라는 사실을 보여준다.

그래서, 이를 통하여, 많은 Idea들은 queue-length-based의 처리량최적화와 안정성에 초점을 맞추어 opportunistic scheduling schemes이 개발 되어왔다. [16]-[20]

(예를 들어), 논문 [16],[17]에서 아래의 form을 따르는 간단한 index 스케줄링 법들은 최적의 처리량을 보여준다.

: 상수, : the head-of-the-line packet delay at queue, : the data rate of user.

그리고 delay-based 정책지표는 지수함수 가중치로 최적의 처리량을 보여준다.

최적의 처리량 스케줄링 법은 [21] 논문을 참고하길 바란다. 논문의 저자는 유저들이 시스템에 도달하는 임의의 부하의 양과 전송개시 하는 부하의 양을 모델링 했다. 그리고 최근에 논문[22], [23]에서의 저자는 큰 traffic 제한성들과 큰 편차로부터의 QoS를 사용하는 기술과 안정성 기반의 다른 형태의 스케줄링을 특징짓고 구분하기를 시도하였다. 이 핵심은 finite-Backlog Case에서 delay 제한성의 조건만 가질 때 QLB(큐 길이 기반) 의 중요성이라는 결과로 이어진다. QLB 정책의 네트워크 처리량은 그렇지 않는 스케줄링 법보다 더 높은 처리량을 보인다.

게다가, 시스템이 증가하는 경우와 초기에 증가하는 총 네트워크 처리량 정책안에서, 주어진 delay조건을 위반하며,

Moreover, for a given delay violation constraint, when the number of users in the system increases, the total network throughput under policy (1) initially increases, and then eventually decreases to zero, but not so under the QLB policy. This should not be entirely surprising since index policies of the form (1) are agnostic to the delays incurred for different users and may not serve users whose queues are building up fast enough to remain within a delay violation probability.

또한 소정의 지연 제약 조건 위반으로 인해 시스템 증가하는 사용자 수가 정책 아래에서의 총 네트워크 처리량이 먼저 상승한 경우 다음 최종적으로 그 QLB 정책에 따라 제로가 아니다. 폼의 인덱스 정책이 다른 사용자 때문에 발생하는 지연에 사로 잡혀 있으면, 큐 지연 위반 확률에 체재하기 위하여 충분한 속도로 구축 된 사용자에게 서비스를 제공하지 않을지도 모르기 때문에 이것은 전혀 놀라운 일이 아니다.

또한, 주어진 지연 위반 제약 조건, 시스템 증가에 있는 사용자의 수가 정책에 따라 전체 네트워크 처리량이 처음 증가 할 때, 그리고 결국 그렇게 QLB 정책 하에서 제로로 감소하지만. 폼의 인덱스 정책이 다른 사용자에 따른 지연 독립적이며, 해당 대기 열 지연 시간 위반 확률 내에 남아있는 만큼 빠르게 구축하는 사용자에게 서비스를 제공 할 수 없습니다 때문에 이것은 전혀 놀라운 일이 안 된다.

..작성중

REFERENCES

[1] F. P. Kelly, A. Maulloo, and D. Tan, “Rate control in communication networks: Shadow prices, proportional fairness and stability,” J. Oper. Res. Soc., vol. 49, pp. 237–252, 1998.

[2] H. Yaiche, R. Mazumdar, and C. Rosenberg, “A game theoretic framework for bandwidth allocation and pricing in broadband networks,” IEEE/ACM Trans. Netw., vol. 8, no. 5, pp. 667–678, Oct. 2000.

[3] S. H. Low and D. E. Lapsley, “Optimization flow control-I: Basic algorithm and convergence,” IEEE/ACM Trans. Netw., vol. 7, no. 6, pp. 861–874, Dec. 1999.

[4] S. Kunniyur and R. Srikant, “End-to-end congestion control schemes: Utility functions, random losses and ECN marks,” in Proc. IEEE INFOCOM, Tel-Aviv, Israel, Mar. 2000, pp. 1323–1332.

[5] S. H. Low and R. Srikant, “A mathematical framework for designing a low-loss low-delay Internet,” Netw. Spatial Econom., vol. 4, no. 1, pp. 75–102, Mar. 2004.

[6] R. Srikant, The Mathematics of Internet Congestion Control. Cambridge, MA: Birkhauser, 2004.

[7] M. Chiang, S. H. Low, R. A. Calderbank, and J. C. Doyle, “Layering as optimization decomposition,” Proc. IEEE, Dec. 2006, to be published.

[8] R. Knopp and P. Humblet, “Information capacity and power control in single-cell multiuser communications,” in Proc. ICC, 1995, pp. 331–335.

[9] P. Bender, P. Black, M. Grob, R. Padovani, N. Sindhushayana, and A. Viterbi, “CDMA/HDR: A bandwidth-efficient high-speed wireless data service for nomadic users,” IEEE Commun. Mag., pp. 70–77, Jul. 2000.

[10] S. Borst and P. Whiting, “Dynamic rate control algorithms for HDR throughput optimization,” in Proc. IEEE INFOCOM, Alaska, Apr. 2001, pp. 976–985.

[11] ——, “The use of diversity antennas in high-speed wireless systems: Capacity gains, fairness issues, multi-user scheduling,” Bell Laboratories Technical Memorandum, 2001.

[12] X. Liu, E. K. P. Chong, and N. B. Shroff, “Opportunistic transmission scheduling with resource-sharing constraints in wireless networks,” IEEE J. Sel. Areas Commun., vol. 19, no. 10, pp. 2053–2064, Oct. 2001.

[13] ——, “A framework for opportunistic scheduling in wireless networks,” Comput. Netw., vol. 41, no. 4, pp. 451–474, Mar. 2003.

[14] A. Jalali, R. Padovani, and R. Pankaj, “Data throughput of CDMA-HDR a high efficiency-high data rate personal communication wireless system,” in Proc. IEEE Veh. Technol. Conf., 2000, pp. 1854–1858.

[15] L. Tassiulas and A. Ephremides, “Stability properties of constrained queueing systems and scheduling policies for maximum throughput in multihop radio networks,” IEEE Trans. Autom. Control, vol. 37, no. 12, pp. 1936–1948, Dec. 1992.

[16] M. Andrews, K. Kumaran, K. Ramanan, A. Stolyar, P. Whiting, and R. Vijayakumar, “Providing quality of service over a shared wireless link,” IEEE Commun. Mag., vol. 39, pp. 150–153, Feb. 2001.

[17] S. Shakkottai and A. Stolyar, “Scheduling for multiple flows sharing a time-varying channel: The exponential rule,” Translations of the AMS, 2001, a volume in memory of F. Karpelevich.

[18] ——, “Scheduling of a shared a time-varying channel: The exponential rule stability,” in Proc. INFORMS Appl. Prob. Conf., New York, Jul. 2001.

[19] R. Buche and H. J. Kushner, “Control of mobile communication systems with time-varying channels via stability methods,” IEEE Trans. Autom. Control, vol. 49, no. 11, pp. 1954–1962, Nov. 2004.

[20] A. L. Stolyar, “Maximizing queueing network utility subject to stability: Greedy primal-dual algorithm,” Queueing Syst., vol. 50, no. 4, pp. 401–457, 2005.

[21] S. Borst, “User-level performance of channel-aware scheduling algorithms in wireless data networks,” IEEE/ACM Trans. Netw., vol. 13, no. 3, pp. 636–647, Jun. 2005.

[22] S. Shakkottai, “Effective capacity and QoS for wireless scheduling,” preprint, 2004.

[23] L. Ying, R. Srikant, A. Eryilmaz, and G. Dullerud, “A large deviations analysis of scheduling in wireless networks,” Trans. Inf. Theory, 2005, Earlier versions of the paper appeared in the IEEE CDC 2004, IEEE

CDC 2005 and IEEE ISIT 2006, submitted for publication.

[24] S. Sarkar and L. Tassiulas, “End-to-end bandwidth guarantees through fair local spectrum share in wireless ad-hoc networks,” in Proc. IEEE Conf. Decision and Control, Maui, HI, Dec. 2003, pp. 564–569.

[25] Y. Yi and S. Shakkottai, “Hop-by-hop congestion control over a wireless multi-hop network,” in Proc. IEEE INFOCOM, Hong Kong, Mar. 2004, pp. 2548–2558.

[26] Y. Xue, B. Li, and K. Nahrstedt, “Price-based resource allocation in wireless ad hoc networks,” in Proc. 11th Int. Workshop on Quality of Service, also Lecture Notes in Computer Science. New York: Springer-Verlag, vol. 2707, Monterey, CA, Jun. 2003, pp. 79–96.

[27] L. Chen, S. H. Low, and J. C. Doyle, “Joint congestion control and media access control design for wireless ad hoc networks,” in Proc. IEEE INFOCOM, Miami, FL, Mar. 2005, pp. 2212–2222.

[28] X. Lin and N. B. Shroff, “Joint rate control and scheduling in multihop wireless networks,” in Proc. IEEE Conf. Decision and Control, Paradise Island, Bahamas, Dec. 2004, pp. 1484–1489.

[29] ——, “The impact of imperfect scheduling on cross-layer rate control in multihop wireless networks,” in Proc. INFOCOM, Miami, FL, Mar. 2005, pp. 1804–1814.

[30] A. Eryilmaz and R. Srikant, “Fair resource allocation in wireless networks using queue-length-based scheduling and congestion control,” in Proc. IEEE INFOCOM, Miami, FL, Mar. 2005, pp. 1794–1803.

[31] A. Eryilmaz and R. Srikant, “Joint congestion control, routing and MACfor stability and fairness in wireless networks,” IEEE J. Sel. Areas Commun., vol. 24, no. 8, pp. 1514–1524, Aug. 2006.

[32] I. Paschalidis, W. Lai, and D. Starobinski, “Asymptotically optimal transmission policies for low-power wireless sensor networks,” in Proc. IEEE INFOCOM, Miami, FL, Mar. 2005, pp. 2458–2469.

[33] M. J. Neely, E. Modiano, and C. Li, “Fairness and optimal stochastic control for heterogeneous networks,” in Proc. IEEE INFOCOM, Miami, FL, Mar. 2005, pp. 1723–1734.

[34] M. Johansson and L. Xiao, “Scheduling, routing and power allocation for fairness in wireless networks,” in Proc. IEEE Veh. Technol. Conf.–Spring, Milan, Italy, May 2004, pp. 1355–1360.

[35] T. Bonald and L. Massoulie, “Impact of fairness on Internet performance,” in Proc. ACM Sigmetrics, Cambridge, MA, Jun. 2001, pp. 82–91.

[36] J. Mo and J.Walrand, “Fair end-to-end window-based congestion control,” IEEE/ACM Trans. Netw., vol. 8, no. 5, pp. 556–567, Oct. 2000.

[37] M. J. Neely, E. Modiano, and C. E. Rohrs, “Dynamic power allocation and routing for time varying wireless networks,” in Proc. IEEE INFOCOM, San Francisco, CA, Apr. 2003, pp. 745–755.

[38] R. L. Cruz and A. V. Santhanam, “Optimal routing, link scheduling and power control in multi-hop wireless networks,” in Proc. IEEE INFOCOM, San Francisco, CA, Apr. 2003, pp. 702–711.

[39] S. Toumpis and A. J. Goldsmith, “Capacity regions for wireless ad hoc networks,” IEEE Trans. Wireless Commun., vol. 2, no. 4, pp. 736–748, Jul. 2003.

[40] X. Lin and N. B. Shroff, “The impact of imperfect scheduling on cross-layer congestion control in wireless networks,” IEEE/ACM Trans. Netw., vol. 14, no. 2, pp. 302–315, Apr. 2006.

[41] G. Sharma, R. R. Mazumdar, and N. B. Shroff, “Maximum weighted matching with interference constraints,” in Proc. IEEE Int. Workshop Foundations and Algorithms ForWireless Networking, Pisa, Italy,Mar. 2006, pp. 70–74.

[42] C. H. Papadimitriou and K. Steiglitz, Combinatorial Optimization: Algorithms and Complexity. Englewood Cliffs, NJ: Prentice-Hall, 1982. LIN et al.: A TUTORIAL ON CROSS-LAYER OPTIMIZATION IN WIRELESS NETWORKS 1463

[43] L. Xiao, M. Johansson, and S. Boyd, “Simultaneous routing and resource allocation via dual decomposition,” in Proc. 4th Asian Control Conf., Singapore, Sep. 2002, pp. 29–34.

[44] M. Chiang, “Balancing transport and physical layer in multihop wireless networks: Jointly optimal congestion and power control,” IEEE J. Sel. Areas Commun., vol. 23, no. 1, pp. 104–116, Jan. 2005.

[45] ——, “Geometric programming for communication systems,” Foundations and Trends in Communications and Information Theory, vol. 2, no. 1–2, pp. 1–154, Jul. 2005.

[46] M. Arisoylu, T. Javidi, and R. L. Cruz, “End-to-end and MAC-layer fair rate assignment in interference limited wireless access networks,” in Proc. IEEE ICC , Istanbul, Turkey, Jun. 2006, to be published.

[47] X. Wang and K. Kar, “Cross-layer rate control for end-to-end proportional fairness in wireless networks with random access,” in Proc. ACM Mobihoc, Urbana-Champaign, IL, May 2005, pp. 157–168.

[48] J. W. Lee, M. Chiang, and R. A. Calderbank, “Jointly optimal congestion and contention control in wireless ad hoc networks,” IEEE Commun. Lett., vol. 10, no. 3, pp. 216–218, Mar. 2006.

[49] J. Zhang and D. Zheng, “A stochastic primal-dual algorithm for joint flow control andMAC design in multi-hop wireless networks,” in Proc. Conf. Inf. Sci. Syst., Princeton, NJ, Mar. 2006.

[50] L. Bui, A. Eryilmaz, R. Srikant, and X. Wu, “Joint congestion control and distributed scheduling in multihop wireless networks with a nodeexclusive interference model,” in Proc. IEEE INFOCOM, 2006.

[51] E. Leonardi, M. Mellia, F. Neri, and M. A. Marsan, “On the stability of input-queued switches with speed-up,” IEEE/ACM Trans. Netw., vol. 9, no. 1, pp. 104–118, Feb. 2001.

[52] X. Wu and R. Srikant, “Regulated maximal matching: A distributed scheduling algorithm for multi-hop wireless networks with node-exclusive spectrum sharing,” in Proc. IEEE Conf. Decision Control, 2005, pp. 5342–5347.

[53] T. Weller and B. Hajek, “Scheduling non-uniform traffic in a packetswitching system with small propagation delay,” IEEE/ACM Trans. Netw., pp. 813–823, Dec. 1997.

[54] J. Dai and B. Prabhakar, “The throughput of data switches with and without speedup,” in Proc. IEEE INFOCOM, 2000, pp. 556–564.

[55] X. Wu, R. Srikant, and J. R. Perkins, “Queue-length stability of maximal greedy schedules in wireless network,” in Proc. Inf. Theory Appl. Inaugural Workshop, Feb. 2006, Univ. California, San Diego.

[56] P. Chaporkar, K. Kar, and S. Sarkar, “Achieving queue length stability through maximal scheduling in wireless networks,” in Proc. Inf. Theory Appl. Inaugural Workshop, Feb. 2006, Univ. California,

San Diego.

[57] ——, “Throughput guarantees in maximal scheduling in wireless networks,” in Proc. 43rd Annu. Allerton Conf. Commun., Control, Comput., Monticello, IL, Sep. 2005.

[58] X. Lin and S. Rasool, “Constant-time distributed scheduling policies for ad hoc wireless networks,” IEEE CDC 2006. [Online]. Available: http://min.ecn.purdue.edu/~linx/papers.html, submitted for publication

[59] X. Lin, N. Shroff, and R. Srikant, “On the connection-level stability of congestion-controlled communication networks,” IEEE Trans. Inf. Theory, 2006, submitted for publication.

[60] P. R. Kumar and T. I. Seidman, “Dynamic instabilities and stabilization methods in distributed real-time scheduling of manufacturing systems,” IEEE Trans. Autom. Control, pp. 289–298, Mar. 1990.

[61] A. Rybko and A. Stolyar, “Ergodicity of stochastic processes describing the operation of open queueing networks,” Problems of Information Transmission, vol. 28, pp. 199–220, 1992, translated from

Problemy Peredachi Informatsii, vol. 28, no. 3, pp. 3–26, 1992.

[62] A. Eryilmaz, E. Modiano, and A. Ozdaglar, “Distributed control for throughput-optimality and fairness in wireless networks,” preprint, 2006.

[63] Y. Yi, G. de Veciana, and S. Shakkottai, “Learning contention patterns and adapting to load/topology changes in a MAC scheduling algorithm,” preprint, 2006.

[64] J.-W. Lee, R. R. Mazumdar, and N. B. Shroff, “Downlink power allocation for multi-class CDMA wireless networks,” in Proc. IEEE INFOCOM, 2002, vol. 3, pp. 1480–1489.

[65] ——, “Opportunistic power scheduling for multi-server wireless systems with minimum performance constraints,” in Proc. IEEE INFOCOM, Hong Kong, China, 2004, pp. 1067–1077.

[66] M. Chiang, S. Zhang, and P. Hande, “Distributed rate allocation for inelastic flows: Optimization frameworks, optimality conditions, and optimal algorithms,” in Proc. IEEE INFOCOM,Miami, FL, Mar. 2005,

pp. 2679–2690.

저작자표시

'N.&C. > Optimization' 카테고리의 다른 글

[Lagrangian] 라그랑지언 (0)	2013.07.09
LMS 알고리즘 (1)	2013.06.10

[Lagrangian] 라그랑지언

2013. 7. 9. 20:43

** 본 내용은 위키 피디아의 내용을 토대로 정리하였습니다.**

출처 : http://ko.wikipedia.org/wiki/%EB%9D%BC%EA%B7%B8%EB%9E%91%EC%A7%80%EC%95%88

Lagrangian를 이해하기 위해서 그것이 대표적으로 쓰인 라그랑주 역학을 알면 쉽게 접근이 가능하다.

예를들어, 라그랑주 역학에서는 라그랑지언(= 시스템의 동역학을 나태내는 함수를 말한다) 함수를 구하여 라그랑주 방정식 (=오일러-라그랑주 방정식) 넣어서 풀면 물체의 궤적을 알수있는 식을 구할수가 있다.

이는 라그랑지언을 어디에 사용하는가에 따라서 다양한 적용이 가능하는 뜻이다.

그러므로, 라그랑지안은 하나의 테크닉이며, 수학적 기법이라고 할수가 있는 것이다.

[경제학에서의 라그랑지안] -- 출처 : http://economia.tistory.com/2

라그랑주 역학(Lagrangian mechanics)은 조제프 루이 라그랑주가 고전역학을 새롭게 공식화하여 그의 논문 《해석 역학》을 통해 1788년에 발표한 이론이다. 라그랑주 역학에서는 라그랑지언을 구해 라그랑주 방정식에 넣어 풀어냄으로써 물체의 궤적을 구할 수 있다.

**라그랑주 방정식**

라그랑주 역학의 운동방정식을 라그랑주 방정식(Lagrange's equation)이라고 한다. 자세한 형태는 아래와 같다.

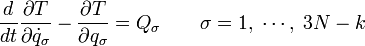
${d \over dt} {\partial T \over \partial \dot{q}_\sigma} - {\partial T \over \partial q_\sigma } = Q_\sigma \qquad \sigma = 1, \; \cdots , \; 3N-k$

보존계의 경우, 라그랑주 방정식은 다음과 같은 형태를 가지고, 이러한 방정식을 오일러-라그랑주 방정식(Euler-Lagrange equation)이라고 한다.

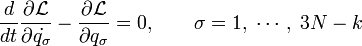
${d \over dt} {\partial \mathcal{L} \over \partial \dot{q_\sigma} } - {\partial \mathcal{L} \over \partial q_\sigma} = 0 , \qquad \sigma = 1, \;\cdots ,\;3N-k$

여기서,

q : 일반화 좌표

σ : 일반화 좌표를 나타내는 지표

N : 입자의 수

k : 홀로노믹 구속의 수

t : 시간

ℒ : 라그랑지언, T-U 로 정의

T : 운동 에너지

U : 퍼텐셜

이다. 보통, 오일러-라그랑주 방정식을 대부분의 라그랑주 역학에서 등장하는 문제를 푸는 데 사용하기 때문에 간단히 오일러-라그랑주 방정식을 라그랑주 방정식이라 부르는 경우가 많다

라그랑주 역학에서, 라그랑지언(Lagrangian)이란 계의 동역학을 나타내는 함수다. 라그랑주 역학에서는 계의 상태를 일반화 좌표와 일반화 속도로 나타내므로, 라그랑지언은 일반화 좌표와 일반화 속도의 함수다. 조제프루이 라그랑주가 도입하였다. 기호는 대개 L이다.

라그랑주 역학과 뉴턴 역학은 서로 동등하지만, 라그랑주 역학에서는 직교좌표계 뿐만 아니라 임의의 좌표계 (구면좌표계, 원통좌표계 등)를 사용할 수 있어 편리하다.

*계(系, system)는 구성 요소들을 체계적으로 통일한 조직을 일컫는다. 다시 말해, 일정한 구성 요소들을 포함하고 있고 그 구성 요소들 사이의 상호 관계가 분명히 정의되어 있어야 한다. 계의 정의는 이론에 따라 조금씩 달라질 수 있다.

*동역학(動力學, dynamics)은 물리학에서 고전역학의 한 분야로 힘이 물체의 운동에 미치는 영향을 다룬다. 즉 이는 운동학과 정역학의 결합으로 볼 수 있다.

'고전역학의 라그랑지언과 전미분을 포함하는 라그랑지언과의 차이점을 설명' -> 오일렁 라그랑지언을 얻음.

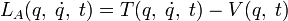어떤 운동방정식을 주는 라그랑지언은 유일하지 않다. 예를 들어, 고전역학의 라그랑지언 $L_A(q,\; \dot{q},\; t) = T(q,\; \dot{q},\; t) - V(q,\; t)$ 와 다음과 같은 좌표와 시간만의 임의의 함수 $f(q,\; t)$ 의 시간에 대한 전미분을 포함하는 라그랑지언

${\mathcal L}_B(q,\; \dot{q},\; t) = {\mathcal L}_A(q,\; \dot{q},\; t) + {d \over dt} f(q, \; t)$

을 비교해보자. 두 이들이 주는 작용의 차이는

$\begin{align} S_B & = \int_{t_1}^{t_2} {L_B(q,\; \dot{q},\; t)} \, dt \\ & = \int_{t_1}^{t_2} {L_A(q,\; \dot{q},\; t)} \, dt + \int_{t_1}^{t_2} {{d \over dt} f(q, \; t)} \, dt \\ & = S_A + \left. f(q,\; t) \right|_{t=t_2} - \left. f(q,\; t)\right|_{t=t_1} \end{align}$

이므로 $\left. f(q,\; t) \right|_{t=t_2} - \left. f(q,\; t)\right|_{t=t_1}$ 만큼 차이가 난다. 하지만 이는 상수이므로 여기에 변분을 취하면

$\delta S_B = \delta S_A + \delta \left[ \left. f(q,\; t) \right|_{t=t_2} - \left. f(q,\; t)\right|_{t=t_1} \right] = \delta S_A$

가 되어 최종적으로 다음과 같은 오일러-라그랑주 방정식을 얻게 되며 두 라그랑지언에 의해 얻게 되는 운동방정식은 같게 된다.

$\frac{d}{d t}\frac{\partial L}{\partial\dot q} = \frac{\partial L}{\partial q}$

일반적으로, 라그랑지언이 어떤 임의의 함수의 전미분만큼 달라도 같은 오일러-라그랑주 방정식을 얻는다.

오일러 - 라그랑지 방정식의 유도과정은 아래와 같다.

Euler-Lagrange Equation

It is a well-known fact, first enunciated by Archimedes, that the shortest distance between two points in a plane is a straight-line. However, suppose that we wish to demonstrate this result from first principles. Let us consider the length, , of various curves, , which run between two fixed points, and , in a plane, as illustrated in Figure 127. Now, takes the form

$\begin{displaymath} l = \int_A^B [dx^2 + dy^2]^{1/2} = \int_a^b [1 + y'^{\,2}(x)]^{1/2}\,dx, \end{displaymath}$

where $y'\equiv dy/dx$ . Note that is a function of the function . In mathematics, a function of a function is termed a functional.

**Figure 127:** *Different paths between points and.*
$\begin{figure} \epsfysize =2.5in \centerline{\epsffile{AppendixD/figD.01.eps}} \end{figure}$

Now, in order to find the shortest path between points and , we need to minimize the functional with respect to small variations in the function , subject to the constraint that the end points, and , remain fixed. In other words, we need to solve

$\begin{displaymath} \delta l = 0. \end{displaymath}$

The meaning of the above equation is that if $y(x)\rightarrow y(x)+\delta y(x)$ , where $\delta y(x)$ is small, then the first-order variation in , denoted $\delta l$ , vanishes. In other words, $l\rightarrow l + {\cal O}(\delta y^{\,2})$ . The particular function for which $\delta l =0$ obviously yields an extremum of (i.e., either a maximum or a minimum). Hopefully, in the case under consideration, it yields a minimum of .

Consider a general functional of the form

$\begin{displaymath} I = \int_a^b F(y, y',x)\,dx, \end{displaymath}$

where the end points of the integration are fixed. Suppose that $y(x)\rightarrow y(x)+\delta y(x)$ . The first-order variation in is written

$\begin{displaymath} \delta I = \int_a^b\left(\frac{\partial F}{\partial y}\,\delta y+ \frac{\partial F}{\partial y'}\,\delta y'\right)dx, \end{displaymath}$

where $\delta y' = d(\delta y)/dx$ . Setting $\delta I$ to zero, we obtain

$\begin{displaymath} \int_a^b\left(\frac{\partial F}{\partial y}\,\delta y+ \frac{\partial F}{\partial y'}\,\delta y'\right)\,dx = 0. \end{displaymath}$

This equation must be satisfied for all possible small perturbations $\delta y(x)$ .

Integrating the second term in the integrand of the above equation by parts, we get

$\begin{displaymath} \int_a^b\left[\frac{\partial F}{\partial y}- \frac{d}{dx}\!\... ... +\left[\frac{\partial F}{\partial y'}\,\delta y\right]_a^b=0. \end{displaymath}$

Now, if the end points are fixed then $\delta y=0$ at and . Hence, the last term on the left-hand side of the above equation is zero. Thus, we obtain

$\begin{displaymath} \int_a^b\left[\frac{\partial F}{\partial y}- \frac{d}{dx}\!\left(\frac{\partial F}{\partial y'}\right)\right]\delta y\,dx =0. \end{displaymath}$

The above equation must be satisfied for all small perturbations $\delta y(x)$ . The only way in which this is possible is for the expression enclosed in square brackets in the integral to be zero. Hence, the functional attains an extremum value whenever

$\begin{displaymath} \frac{d}{dx}\!\left(\frac{\partial F}{\partial y'}\right)-\frac{\partial F}{\partial y} = 0. \end{displaymath}$

This condition is known as the Euler-Lagrange equation.

Let us consider some special cases. Suppose that does not explicitly depend on . It follows that $\partial F/\partial y = 0$ . Hence, the Euler-Lagrange equation (1681) simplifies to

$\begin{displaymath} \frac{\partial F}{\partial y'} = {\rm const}. \end{displaymath}$

Next, suppose that does not depend explicitly on . Multiplying Equation (1681) by , we obtain

$\begin{displaymath} y'\,\frac{d}{dx}\!\left(\frac{\partial F}{\partial y'}\right)-y'\,\frac{\partial F}{\partial y} = 0. \end{displaymath}$

However,

$\begin{displaymath} \frac{d}{dx}\!\left(y'\,\frac{\partial F}{\partial y'}\right... ...l F}{\partial y'}\right)+ y''\,\frac{\partial F}{\partial y'}. \end{displaymath}$

Thus, we get

$\begin{displaymath} \frac{d}{dx}\!\left(y'\,\frac{\partial F}{\partial y'}\right... ...\partial F}{\partial y} + y''\,\frac{\partial F}{\partial y'}. \end{displaymath}$

Now, if is not an explicit function of then the right-hand side of the above equation is the total derivative of , namely . Hence, we obtain

$\begin{displaymath} \frac{d}{dx}\!\left(y'\,\frac{\partial F}{\partial y'}\right) = \frac{dF}{dx}, \end{displaymath}$

which yields

$\begin{displaymath} y'\,\frac{\partial F}{\partial y'} - F = {\rm const}. \end{displaymath}$

Returning to the case under consideration, we have $F = \sqrt{1+y'^{\,2}}$ , according to Equation (1674) and (1676). Hence, is not an explicit function of , so Equation (1682) yields

$\begin{displaymath} \frac{\partial F}{\partial y'} = \frac{y'}{\sqrt{1+y'^{\,2}}} = c, \end{displaymath}$

where is a constant. So,

$\begin{displaymath} y' = \frac{c}{\sqrt{1-c^2}} = {\rm const}. \end{displaymath}$

Of course, $y' = {\rm constant}$ is the equation of a straight-line. Thus, the shortest distance between two fixed points in a plane is indeed a straight-line.

저작자표시

'N.&C. > Optimization' 카테고리의 다른 글

A Tutorial on Cross-Layer Optimization in Wireless Networks (0)	2013.07.23
LMS 알고리즘 (1)	2013.06.10

LMS 알고리즘

2013. 6. 10. 23:56

출처 : 네이버 지식인.

LMS(Least Mean Square)

이 방법은 많은 데이터가 주어졌을때 그 데이터들이 이루는 그래프를

산출해내기 위하여 사용하는 방법들 중 하나입니다.

즉 2차원 데이터들이 다음과 같이 주어졌다고 하면

(1,2) (2,5) (3,8) (4,10) (5,14)

이들이 이루는 1차원 직선을 찾고 싶다면 다음과 같이 가정합니다.

y=ax

이 그래프에 위의 5개의 데이터를 대입하여 a를 찾아내고

그 오차가 가장 적은 a를 선택하는 방법이 LMS입니다.,

이제, 예를 들어 보겠습니다.

출처: WiKi

위 그래프는 위키 백과에서 회귀 분석을 설명할때 사용된 그림입니다.

파란색의 점들이 각각의 샘플들이라면, 이들의 경향성을 따라서 직선을 그은것이 바로 위에서 설명한 LMS 수식으로 표현것입니다. 즉, 아주 간단한 근사화 방법으로써 실제로 많이 쓰이지만 그렇게 정확도가 높지는 않습니다.

이러한 데이터 혹은 샘플 혹은 어떠한 분포도를 하나의 수식으로 표현하기 위해서, 이를 모델화 한다고 합니다. 모델은 우리가 원하는 물리적인 현상을 잘 반영해야 합니다. 하지만 분명 오차가 발생하기 때문에, 이를 최소자승법을 통하여 원하는 결과값이 나오도록 하는 오류를 최소화 하는 변수값을 알아내는것이 핵심입니다.

이를 식으로 다시 이야기 해보겠습니다.

참조 : The Method of Least Squares of Steven J. Miller∗

http://web.williams.edu/Mathematics/sjmiller/public_html/BrownClasses/54/handouts/MethodLeastSquares.pdf