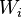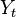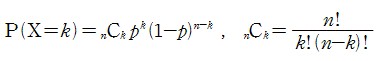Sigma Notation (Summation Notation) and Pi Notation
Sigma (Summation) Notation
is a capital letter from the Greek alphabet called “Sigma”… it corresponds to “S” in our alphabet (think of the starting sound of the word “sigma”). It is used in mathematics to describe “summation”, the addition or sum of a bunch of terms (think of the starting sound of the word “sum”: Sssigma = Sssum).
Sigma can be used all by itself to represent a generic sum… the general idea of a sum, of an unspecified number of unspecified terms:
But this is not something that can be evaluated to produce a specific answer, as we have not been told how many terms to include in the sum, nor have we been told how to determine the value of each term.
A more typical use of Sigma notation will include an integer below the Sigma (the “starting term number”), and an integer above the Sigma (the “ending term number”). In the example below, the exact starting and ending numbers don’t matter much since we are being asked to add the same value, two, repeatedly. All that matters in this case is the difference between the starting and ending term numbers… that will determine how many twos we are being asked to add, one two for each term number.
Sigma notation, or as it is also called, summation notation is not usually worth the extra ink to describe simple sums such as the one above… multiplication could do that more simply.
Sigma notation is most useful when the “term number” can be used in some way to calculate each term. To facilitate this, a variable is usually listed below the Sigma with an equal sign between it an the starting term number. If this variable appears in the expression being summed, then the current term number should be substituted for the variable:
Note that it is possible to have a variable below the Sigma, but never use it. In such cases, just as in the example that resulted in a bunch of twos above, the term being added never changes:
The “starting term number” need not be 1. It can be any value, including 0. For example:
That covers what you need to know to begin working with Sigma notation. However, since Sigma notation will usually have more complex expressions after the Sigma symbol, here are some further examples to give you a sense of what is possible:
Note that the last example above illustrates that, using the commutative property of addition, a sum of multiple terms can be broken up into multiple sums:
And lastly, this notation can be nested:
The rightmost sigma (similar to the innermost function when working with composed functions) above should be evaluated first. Once that has been evaluated, you can evaluate the next sigma to the left. Parentheses can also be used to make the order of evaluation clear.
Pi (Product) Notation
is a capital letter from the Greek alphabet call “Pi”… it corresponds to “P” in our alphabet (think of the starting sound of the word “pi”). It is used in mathematics to represent the product of a bunch of terms (think of the starting sound of the word “product”: Pppi = Ppproduct). It is used in the same way as the Sigma notation described above, except that succeeding terms are multiplied instead of added:
Summary
Sigma (summation) and Pi (product) notation are used in mathematics to indicate repeated addition or multiplication. Sigma notation provides a compact way to represent many sums, and is used extensively when working with Arithmetic or Geometric Series. Pi notation provides a compact way to represent many products.
To make use of them you will need a “closed form” expression (one that allows you to describe each term’s value using the term number) that describes all terms in the sum or product (just as you often do when working with sequences and series). Sigma and Pi notation save much paper and ink, as do other math notations, and allow fairly complex ideas to be described in a relatively compact notation.
깔끔하고 유용한 내용인것 같아서 링크했습니다.
cite: https://mathmaine.wordpress.com/2010/04/01/sigma-and-pi-notation/
'N.&C. > Probability' 카테고리의 다른 글
| [Probability] Renewal theory : 추계적 과정 (0) | 2014.11.03 |
|---|---|
| [independent identically distribution] 독립 동일 분포 (0) | 2014.11.01 |
| [Markov Chain] You_tube Tutorial video. (0) | 2014.10.06 |
| [E-book] Poisson process (0) | 2014.10.06 |
| Markov chain [마코프 체인] (6) | 2013.05.09 |




![0 < \mathbb{E}[S_i] < \infty.](http://upload.wikimedia.org/math/6/4/2/642646acd87e01cd6befabcb8ba03731.png)
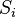

![\mathbb{E}[S_i]](http://upload.wikimedia.org/math/9/2/e/92e2d7bbd26c3eb3dfb9666dad1b61a3.png)
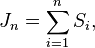


![[J_n,J_{n+1}]](http://upload.wikimedia.org/math/6/b/e/6bec9ae0b54f0d735f3511a0aa7f0507.png)